Una vez finalizado el ejemplo correspondiente al diseño de un tren de engranajes, iniciamos el correspondiente al cálculo de las ruedas y piñones que lo componen.
Lo que hemos hecho hasta el momento ha sido determinar el número de dientes de las ruedas, el número de hojas de los piñones y las velocidades de cada uno de ellos necesarias para que cumplan con los ratios requeridos.
En el ejemplo que nos ocupará a lo largo de los próximos once artículos calcularemos dimensionalmente los valores de todos estos componentes en base a lo obtenido hasta ahora.
Para empezar, precisamos definir una serie de parámetros necesarios para el calculo:
T = número de dientes de la rueda motriz.
t = número de hojas del piñón.
PD = diámetro de paso (Pitch Diameter).
PC = círculo de paso (Pitch Circle). Es el trazado partiendo del diámetro de paso.
PC = CP * T = PD * PI
FD = diámetro completo (Full Diameter) = PD + Adendum.
RC = círculo de base (Root Circle)
CP = paso circular (Circular Pitch). Arco correspondiente a diente más espacio.
CP/2 = anchura del diente = anchura del espacio entre dientes.
M = módulo.
CD = Pitch Centres (distancia entre los centros de la rueda y el piñón).
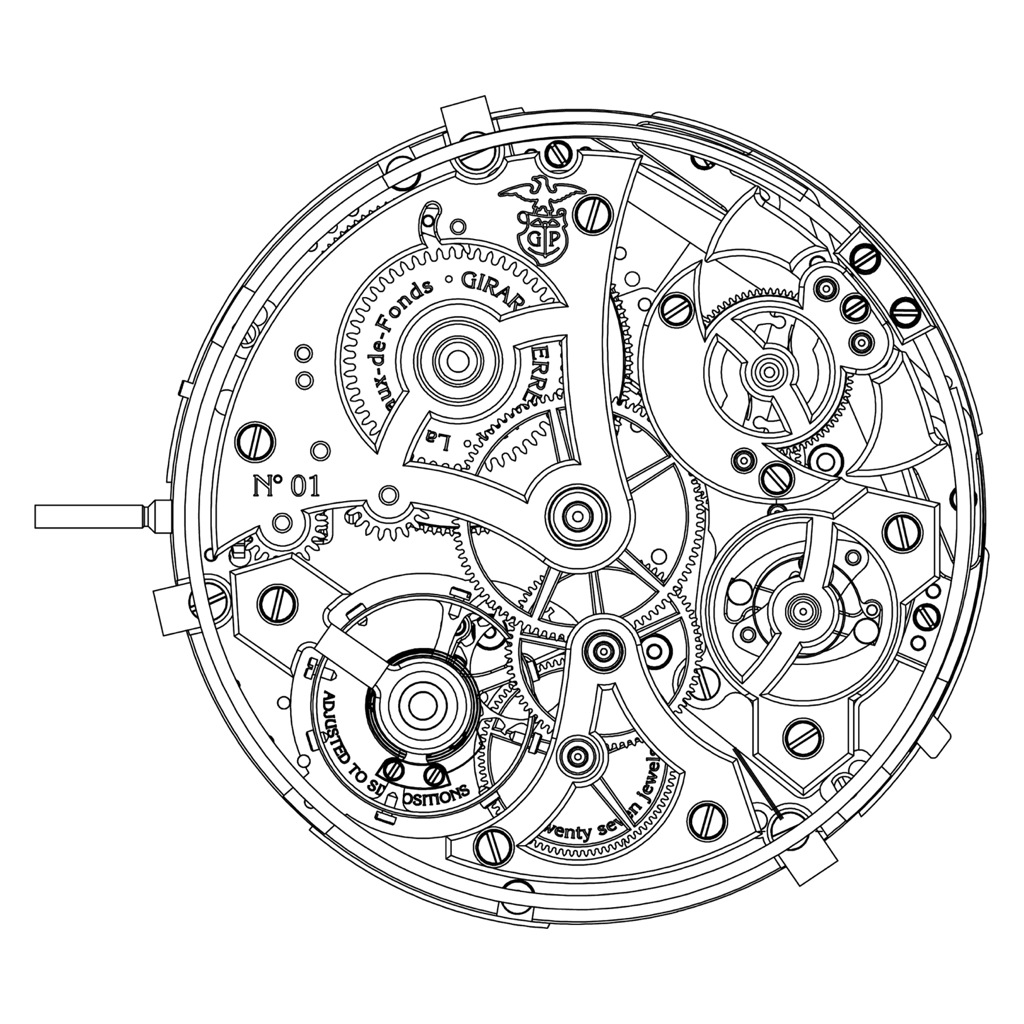
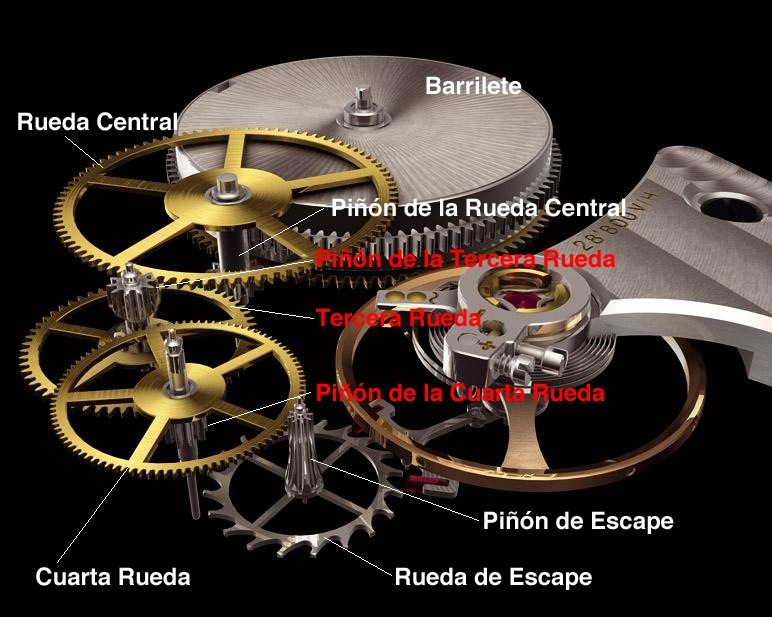
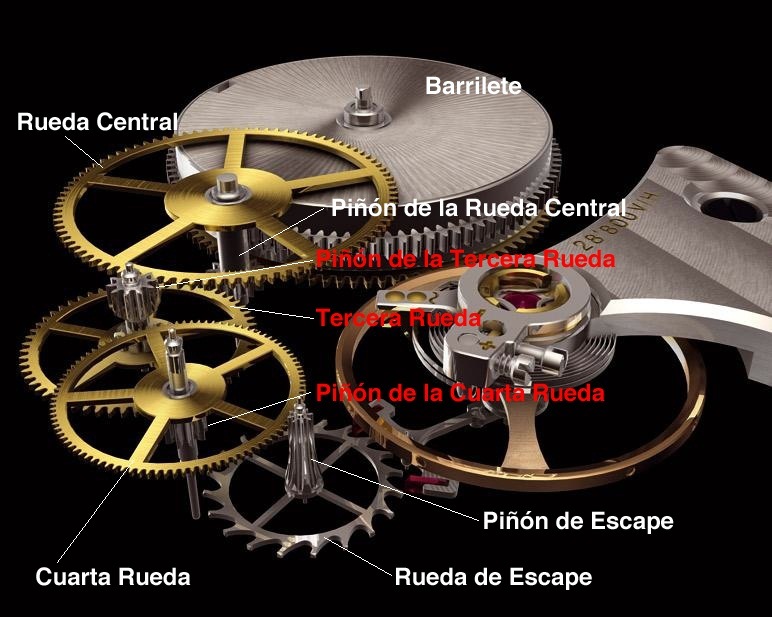
Layout de un reloj convencional.
El layout de un reloj convencional es el mostrado en la siguiente figura.
En el presente ejemplo nos dedicaremos a determinar los siguientes valores para todas las ruedas y piñones del movimiento:
PD (diámetro de paso).
FD (diámetro completo).
T (número de dientes).
t (número de hojas).
Ancho de los dientes.
Ancho de las hojas.
Backlash.
En el ejemplo anterior se han determinado los ratios más adecuados de manera que sean lo suficientemente similares entre ellos para que el ratio global del movimiento se reparta de manera lo más uniforme posible por todo el tren de engranajes.
Para dibujar el anterior layout, los diámetros de las ruedas se han escogido de manera proporcional para que encajen en el espacio disponible sin que se amontonen ni se solapen entre ellas.
Una gran superficie de la pletina base debe permanecer libre para permitir la ubicación de bases seguras para los puentes y los pivotes. Estas zonas se han indicado mediante una línea de puntos con el fin de mostrar los espacios libres o disponibles para los diámetros de las ruedas.
Los círculos dibujados representando las ruedas son los círculos de paso con sus correspondientes diámetros de paso, que se incrementarán hasta sus diámetros completos cuando se incluyan los adendums de los dientes. Es muy importante tener en cuenta este incremento en el momento de decidir el tamaño relativo de las ruedas.
Se puede observar que, al situar los adendums sobre la rueda central y sobre la cuarta rueda, se incurriría en un solapamiento de los dientes. En este caso concreto no importa puesto que la cuarta rueda está por debajo del nivel de la rueda central.
No sucede lo mismo entre la cuarta rueda y el piñón de la tercera. En el dibujo existe un amplio espacio entre el círculo de paso de la cuarta rueda y el correspondiente al piñón de la tercera rueda. Se podría pensar que esta cuarta rueda podría ser mayor, pero no es así puesto que cuando se añade el adendum a los dientes de la cuarta rueda y las extensiones a las hojas del piñón de la tercera rueda, este espacio será mínimo.
Es conveniente hacer el dibujo a gran escala. En este ejemplo, para un calibre de 60 milímetros de diámetro, una escala 2:1 es suficiente.
Los valores de los diámetros de paso se toman directamente midiendo sobre el dibujo así que, para calibres de menor diámetro, será conveniente aumentar la escala.
El procedimiento para el cálculo de los parámetros de cada rueda y piñón del engranaje es el siguiente:
- En primer lugar se mide, sobre el layout, el diámetro de la rueda dibujada. Este diámetro corresponde al diámetro de la rueda.
- Considerando el diámetro de paso anterior y teniendo en cuenta los ratios de transmisión calculados en el ejemplo anterior, se determina el diámetro de paso del piñón conducido por la rueda.
- Se calculan las anchuras de dientes y hojas.
